ddroy_course: July 2022

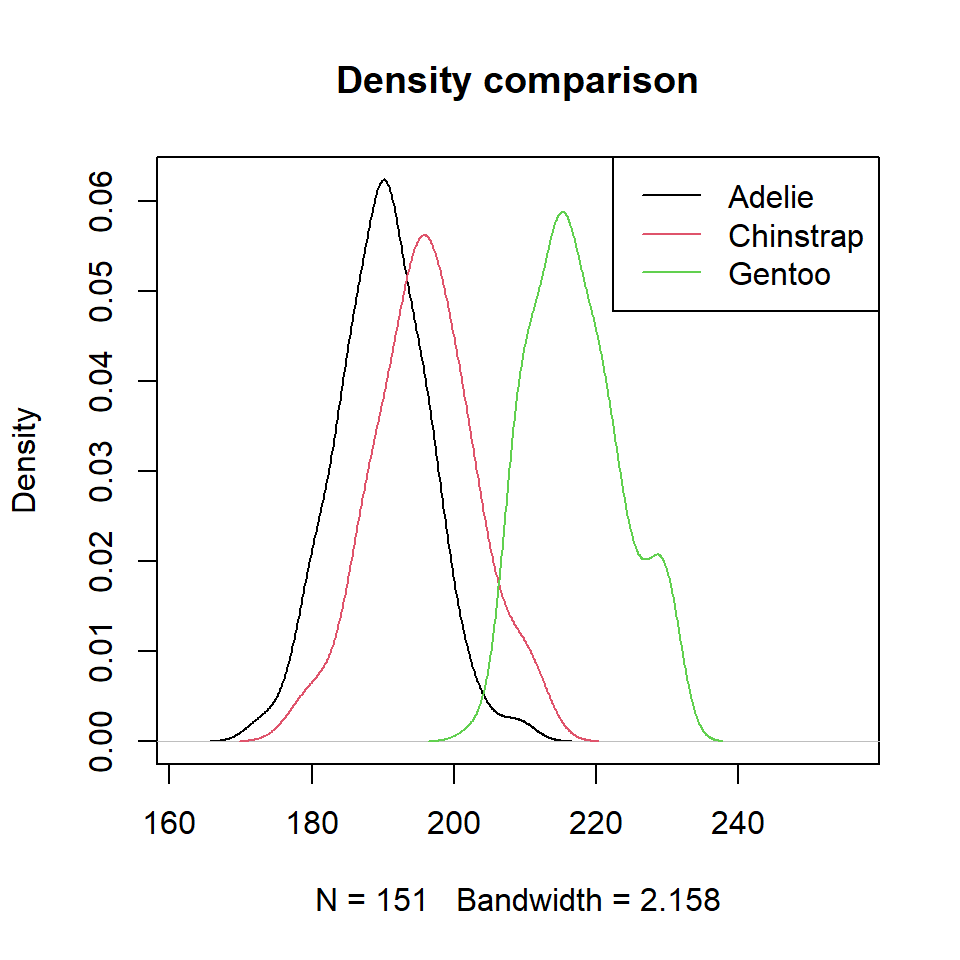
R-Programming

drive

Chapter 1: Download

link: https://youtu.be/cX532N_XLIs

Chapter 2: Vectors

Vectors are the most basic R data objects and there are six types of atomic vectors. They are logical, integer, double, complex, character and raw.

A logical vector is a vector that only contains TRUE and FALSE values. In R, true values are designated with TRUE, and false values with FALSE. When you index a vector with a logical vector, R will return values of the vector for which the indexing vector is TRUE.

Logical : > 10>20

[1] FALSE

Vector manipulation

v1 <- c(3,8,4,5,0,11)
v2 <- c(4,11,0,8,1,2)

v1+v2, v1-v2, v1*v2, v1/v2

v <- c(3,8,4,5,0,11, -9, 304)

# Sort the elements of the vector.
sort.result <- sort(v)
print(sort.result)

# Sort the elements in the reverse order.
revsort.result <- sort(v, decreasing = TRUE)
print(revsort.result)

# Sorting character vectors.
v <- c("Red","Blue","yellow","violet")
sort.result <- sort(v)
print(sort.result)

# Sorting character vectors in reverse order.
revsort.result <- sort(v, decreasing = TRUE)

print(revsort.result)

Data frame

BMI <- 	data.frame(
   gender = c("Male", "Male","Female"), 
   height = c(152, 171.5, 165), 
   weight = c(81,93, 78),
   Age = c(42,38,26)
)
print(BMI)

# Create a matrix.
M = matrix( c('a','a','b','c','b','a'), nrow = 2, ncol = 3, byrow = TRUE)
print(M)

Sequence

> a=seq(1,10, by=0.5)

> a

[1] 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0 5.5 6.0 6.5 7.0 7.5 8.0 8.5 9.0 9.5 10.0

a=seq(10,1)

a=seq(10,1, by= -0.5)

> a

[1] 10.0 9.5 9.0 8.5 8.0 7.5 7.0 6.5 6.0 5.5 5.0 4.5 4.0 3.5 3.0 2.5 2.0 1.5 1.0

stacked bar

A stacked bar graph (or stacked bar chart) is a chart that uses bars to show comparisons between categories of data, but with ability to break down and compare parts of a whole. Each bar in the chart represents a whole, and segments in the bar represent different parts or categories of that whole

Descriptive statistics summarizes or describes the characteristics of a data set.
Descriptive statistics consists of two basic categories of measures: measures of central tendency and measures of variability (or spread).
Measures of central tendency describe the center of a data set.
Measures of variability or spread describe the dispersion of data within the set.

Types of Descriptive Statistics

All descriptive statistics are either measures of central tendency or measures of variability, also known as measures of dispersion.

Central Tendency

Measures of central tendency focus on the average or middle values of data sets, whereas measures of variability focus on the dispersion of data. These two measures use graphs, tables and general discussions to help people understand the meaning of the analyzed data.
Measures of central tendency describe the center position of a distribution for a data set. A person analyzes the frequency of each data point in the distribution and describes it using the mean, median, or mode, which measures the most common patterns of the analyzed data set.

Measures of Variability

Measures of variability (or the measures of spread) aid in analyzing how dispersed the distribution is for a set of data. For example, while the measures of central tendency may give a person the average of a data set, it does not describe how the data is distributed within the set.
So while the average of the data maybe 65 out of 100, there can still be data points at both 1 and 100. Measures of variability help communicate this by describing the shape and spread of the data set. Range, quartiles, absolute deviation, and variance are all examples of measures of variability.
Consider the following data set: 5, 19, 24, 62, 91, 100. The range of that data set is 95, which is calculated by subtracting the lowest number (5) in the data set from the highest (100).

provides a wide range of functions for obtaining summary statistics. One method of obtaining descriptive statistics is to use the sapply( ) function with a specified summary statistic.
`# get means for variables in data frame mydata # excluding missing values sapply(mydata, mean, na.rm=TRUE)`
Possible functions used in sapply include mean, sd, var, min, max, median, range, and quantile.

The t.test( ) function produces a variety of t-tests. Unlike most statistical packages, the default assumes unequal variance and applies the Welsh df modification.`# independent 2-group t-test t.test(y~x) # where y is numeric and x is a binary factor`
`# independent 2-group t-test t.test(y1,y2) # where y1 and y2 are numeric`
`# paired t-test t.test(y1,y2,paired=TRUE) # where y1 & y2 are numeric`
`# one sample t-test t.test(y,mu=3) # Ho: mu=3`
You can use the var.equal = TRUE option to specify equal variances and a pooled variance estimate. You can use the alternative="less" or alternative="greater" option to specify a one tailed test.

t-test

A t-test is a type of inferential statistic used to determine if there is a significant difference between the means of two groups, which may be related in certain features.
The t-test is one of many tests used for the purpose of hypothesis testing in statistics.
Calculating a t-test requires three key data values. They include the difference between the mean values from each data set (called the mean difference), the standard deviation of each group, and the number of data values of each group.
There are several different types of t-test that can be performed depending on the data and type of analysis required.

The Shapiro–Wilk test is a test of normality in frequentist statistics. It was published in 1965 by Samuel Sanford Shapiro and Martin Wilk.

The independent-samples test can take one of three forms, depending on the structure of your data and the equality of their variances. The general form of the test is t. test(y1, y2, paired=FALSE) . By default, R assumes that the variances of y1 and y2 are unequal, thus defaulting to Welch's test.

A Shapiro-Wilk test is the test to check the normality of the data. The null hypothesis for Shapiro-Wilk test is that your data is normal, and if the p-value of the test if less than 0.05, then you reject the null hypothesis at 5% significance and conclude that your data is non-normal.

The Shapiro-Wilk’s test or Shapiro test is a normality test in frequentist statistics. The null hypothesis of Shapiro’s test is that the population is distributed normally. It is among the three tests for normality designed for detecting all kinds of departure from normality. If the value of p is equal to or less than 0.05, then the hypothesis of normality will be rejected by the Shapiro test. On failing, the test can state that the data will not fit the distribution normally with 95% confidence. However, on passing, the test can state that there exists no significant departure from normality. This test can be done very easily in R programming.

shapiro.test(x)

Here, we’ll describe how to create quantile-quantile plots in R. QQ plot (or quantile-quantile plot) draws the correlation between a given sample and the normal distribution. A 45-degree reference line is also plotted. QQ plots are used to visually check the normality of the data.

qqnorm(): produces a normal QQ plot of the variable
qqline(): adds a reference line

qqnorm(my_data$len, pch = 1, frame = FALSE)
qqline(my_data$len, col = "steelblue", lwd = 2)

A paired t-test is used when you survey one group of people twice with the same survey. This type of t-test can show you whether the mean (average) has changed between the first and second time they took the survey.

Data in two numeric vectors # ++++++++++++++++++++++++++ # Weight of the mice before treatment before <-c(200.1, 190.9, 192.7, 213, 241.4, 196.9, 172.2, 185.5, 205.2, 193.7) # Weight of the mice after treatment after <-c(392.9, 393.2, 345.1, 393, 434, 427.9, 422, 383.9, 392.3, 352.2) # Create a data frame my_data <- data.frame( group = rep(c("before", "after"), each = 10), weight = c(before, after)

>Compute t-test res <- t.test(weight ~ group, data = my_data, paired = TRUE)

>res

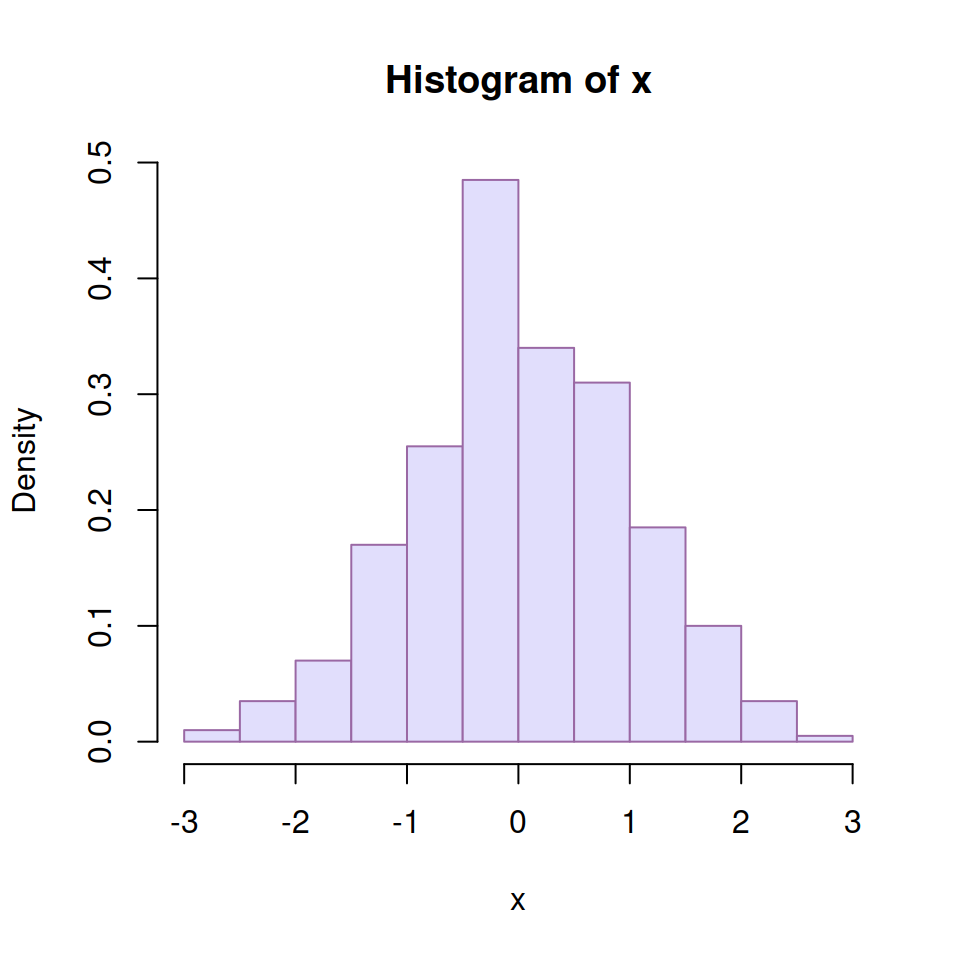
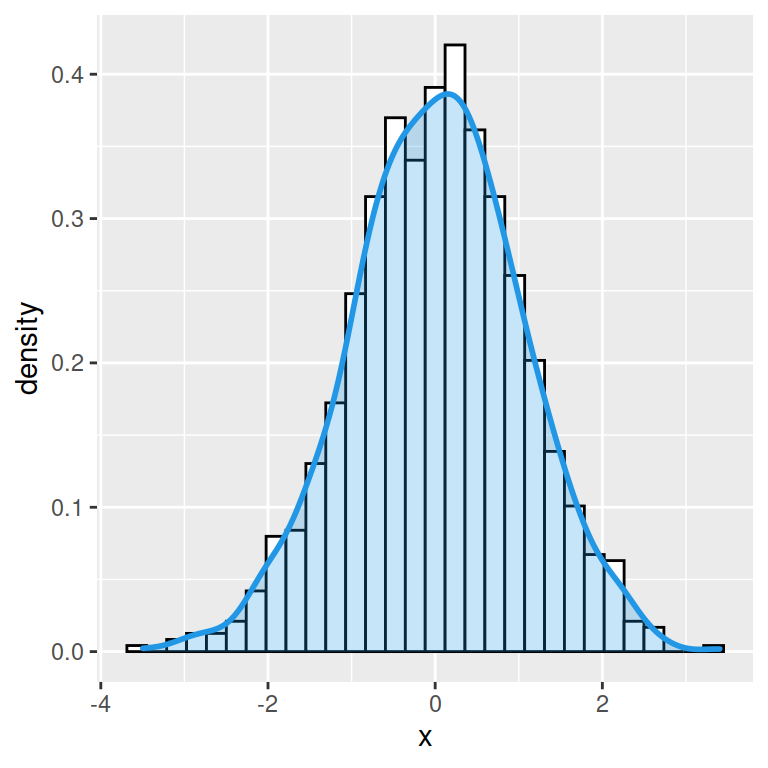
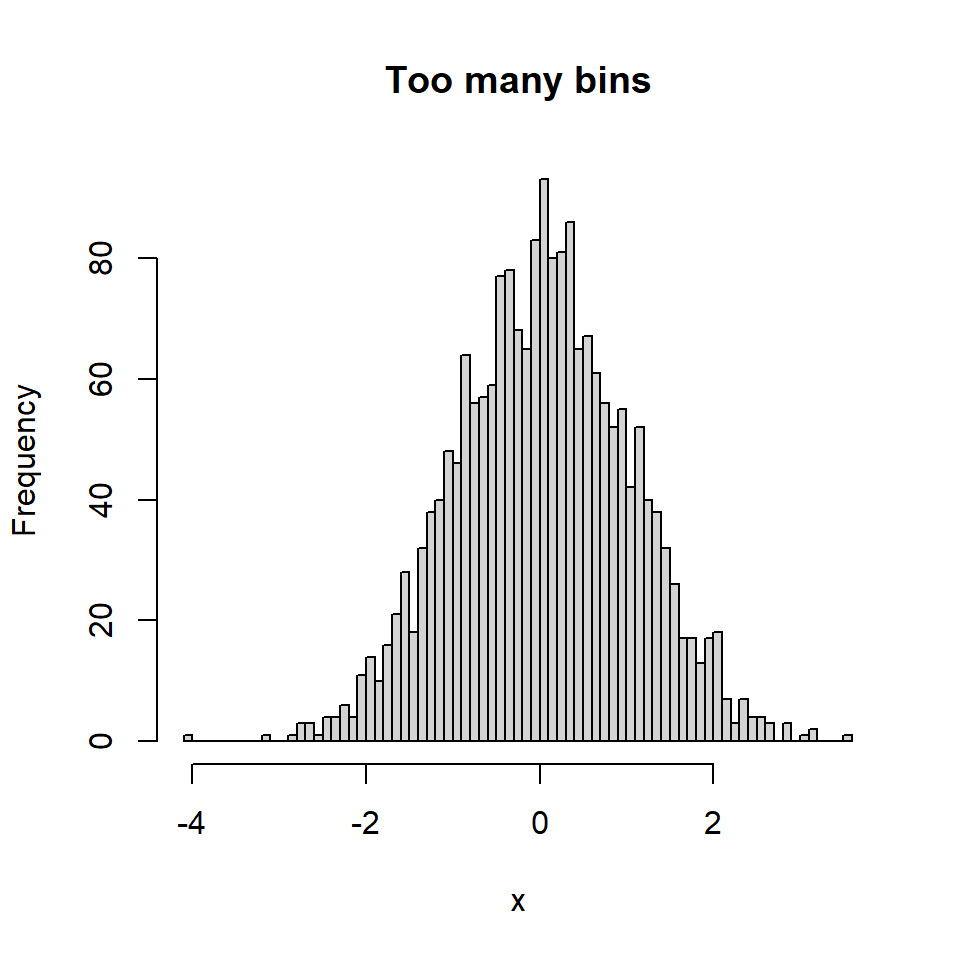
A basic histogram can be created with the hist function. In order to add a normal curve or the density line you will need to create a density histogram setting prob = TRUE as argument.

# Sample data
set.seed(3)
x <- rnorm(200)

# Histogram
hist(x, prob = TRUE)

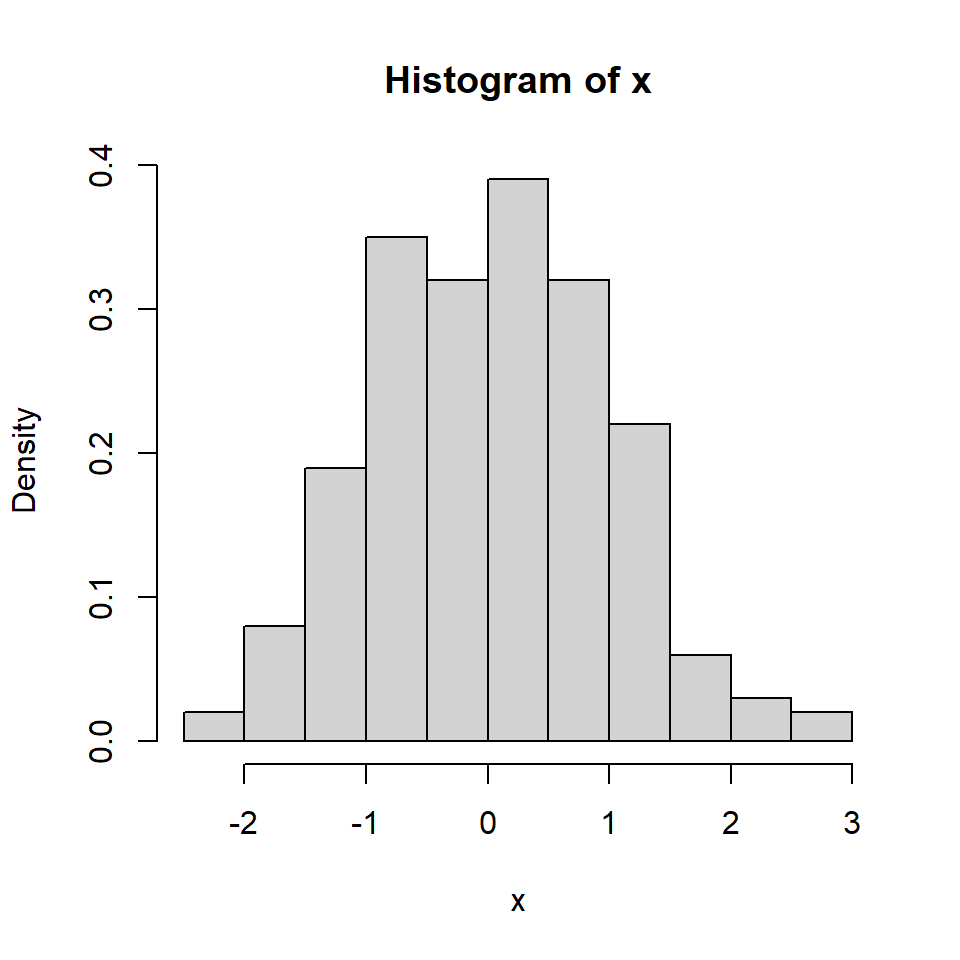
Basic histogram in R

Histogram with normal curve

Histogram with normal curve in R

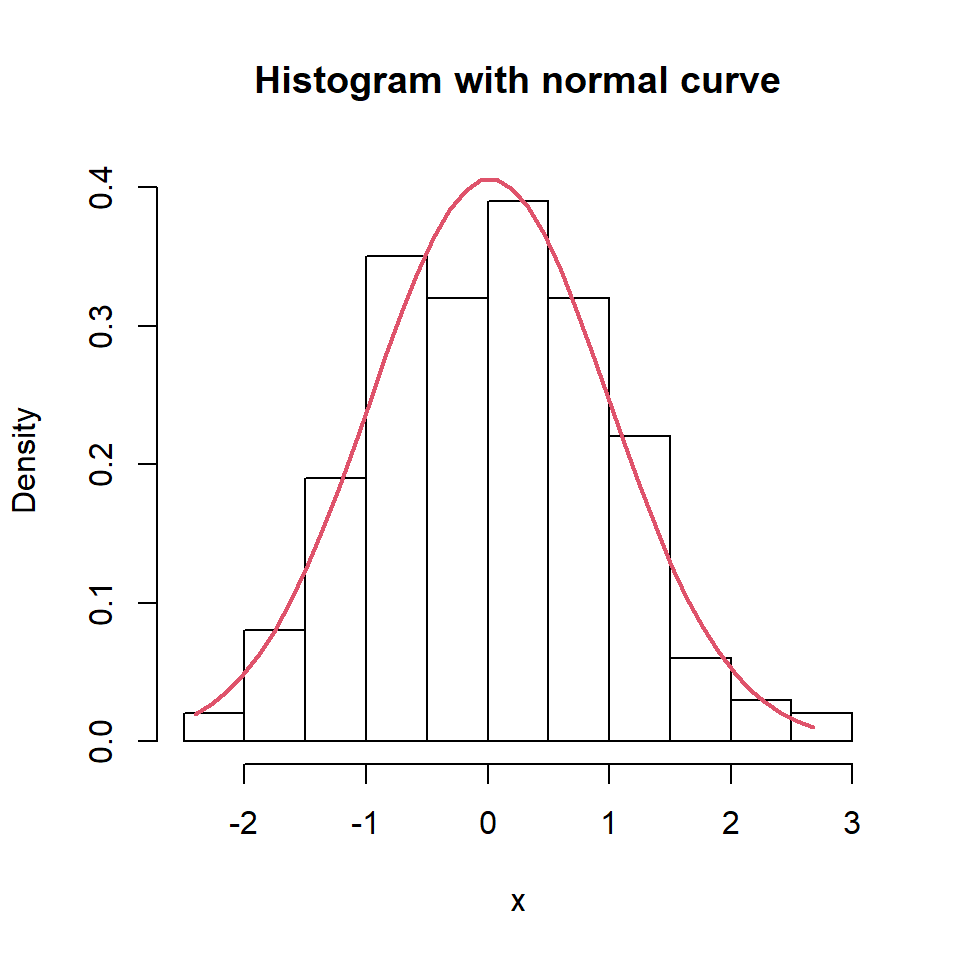
If you want to overlay a normal curve over your histogram you will need to calculate it with the dnorm function based on a grid of values and the mean and standard deviation of the data. Then you can add it with lines.

# X-axis grid
x2 <- seq(min(x), max(x), length = 40)

# Normal curve
fun <- dnorm(x2, mean = mean(x), sd = sd(x))

# Histogram
hist(x, prob = TRUE, col = "white",
     ylim = c(0, max(fun)),
     main = "Histogram with normal curve")
lines(x2, fun, col = 2, lwd = 2)

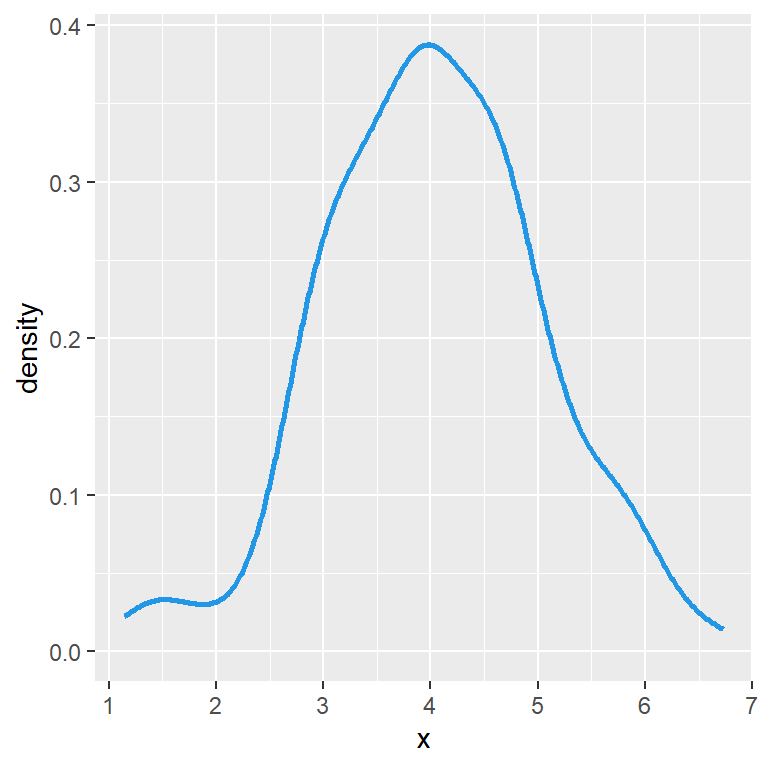
Histogram with density line

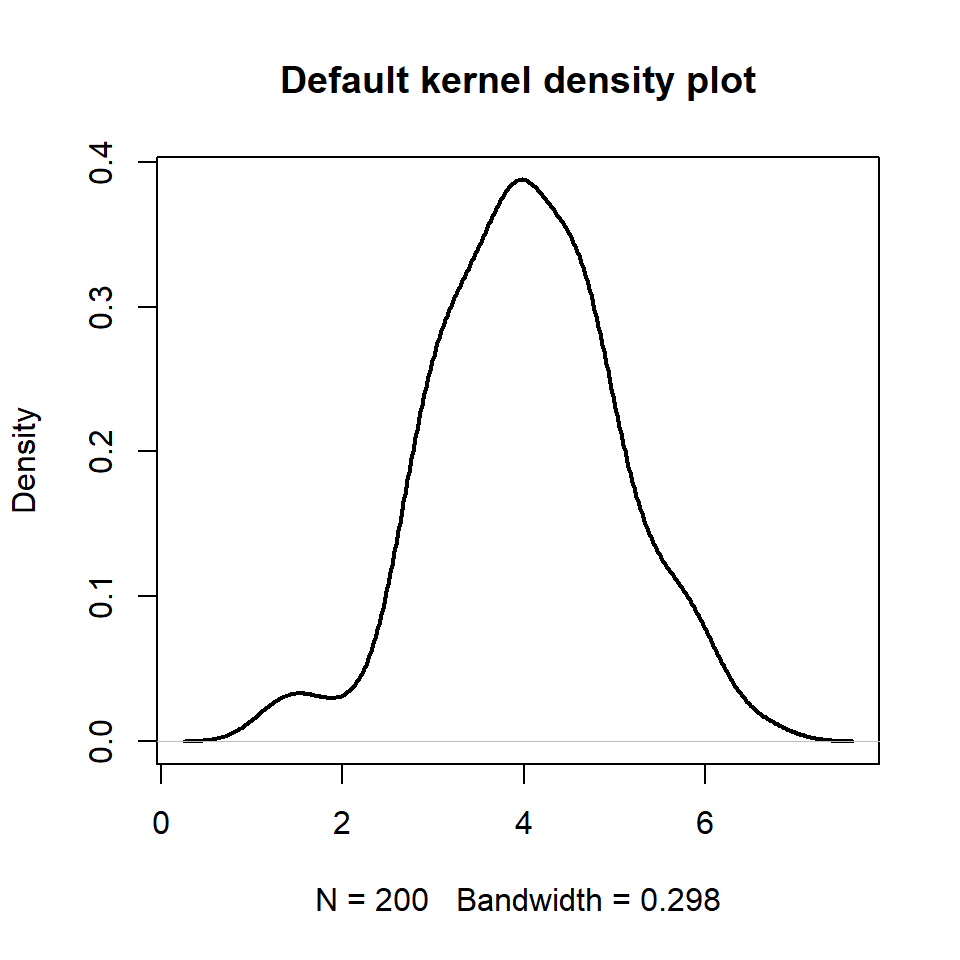
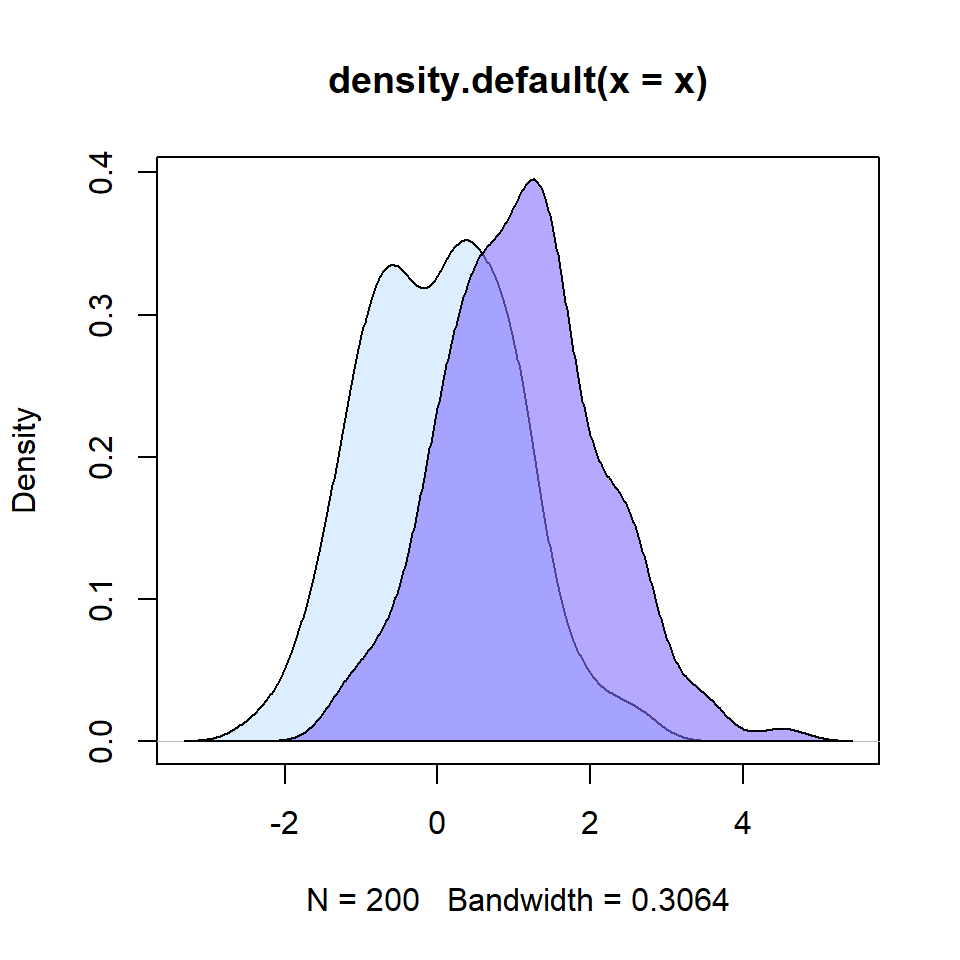
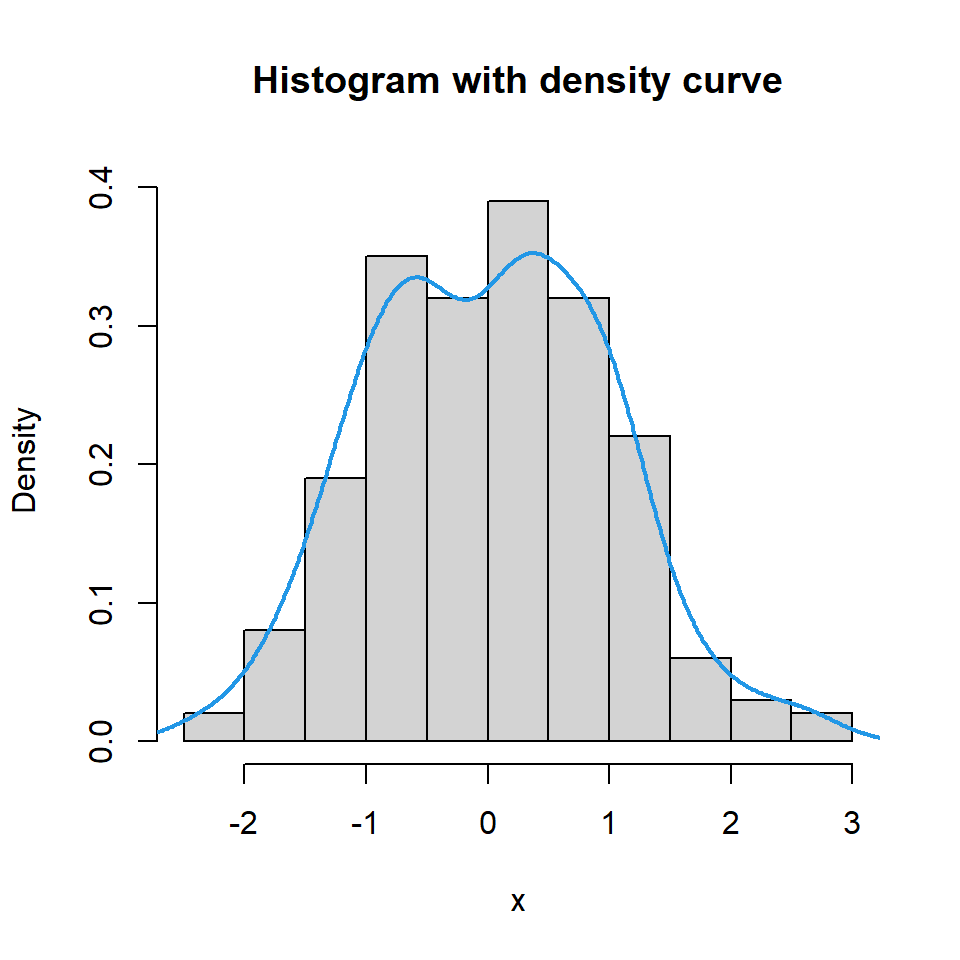
If you prefer adding the density curve of the data you can make use of the density function as shown in the example below.

# Sample data
set.seed(3)
x <- rnorm(200)

# Histogram
hist(x, prob = TRUE, ylim = c(0, max(fun)),
     main = "Histogram with density curve")
lines(density(x), col = 4, lwd = 2)